具有负载边界的一致性哈希(译文)
运行大规模 Web 服务(如内容托管),必然需要负载均衡 —— 将大量客户端(流量)均匀地分发到众多服务器上,以避免出现某台服务器过载。此外,在客户端和服务器都可以随时添加或删除的动态环境中,期望仍能找到一种不随时间波动很大的负载分配策略。换句话说,我们需要将服务器的得到的客户端(流量)分配,随着时间的推移保持一致性。
背景
尽管一致性哈希的概念过去已经演变为处理动态环境中的负载均衡问题,但所有先前研发方案普遍存在的一个根本问题是,在某些场景下,它们可能会导致许多服务器上的负载均衡不理想。
此外,客户端和服务器都可能会定期添加或删除,但我们(谷歌研究团队,下同)不希望通过此类更改移动大量客户端。 因此,动态分配算法不仅要始终确保适当的负载均衡,它还应该最大限度地减少每次更改系统后被移动的客户端数量。 当我们面临对每台服务器容量的严格限制时,这种分配问题变得更加具有挑战性 —— 也就是说,每台服务器都有一个最大负载容量。 通常情况下,我们希望容量能接近平均负载。
换句话说,我们期望同时实现结果分配的统一性和一致性。有大量的文献介绍了较为简单场景的解决方案, 即服务器集群是固定的,只有客户端集群被更新。但在本文中,我们讨论完全动态场景下的解决方案,即客户端和服务器可以随时被添加和删除。
算法
我们可以把每个客户端看作是一只球,把服务器看作是装球的桶,类似于经过充分研究的 balls-to-bins 随机过程中的符号。为了实现桶中球的均匀性,追求所有桶的负载尽量接近平均负载(球的数量除以桶的数量)。对于某个参数 ε,我们设置每个桶的容量为平均负载(1+ε)倍的向下或向上取整值。这种容量范围使我们能够设计一种分配算法,同时满足均匀性和一致性的目标。
设想一组给定范围的数字,叠加在一个圆环上。我们对球使用哈希函数,并对桶使用另外的哈希函数,以取得给定范围内与该圆环上的位置相对应的数字。然后,我们开始以特定的顺序(假设根据它们的 ID,而不是它们的哈希值)分配球。 然后每个球沿着圆环顺时针移动,直到有空余容量的第一个桶,并分配到这个桶。
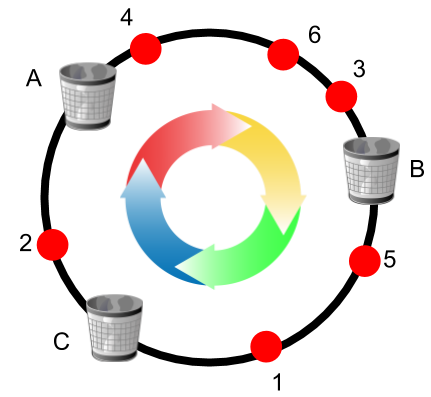
如上图所示,将 6 个球和 3 个桶分别使用两个独立的哈希函数,将它们随机循环分配到圆环上的桶。 在这个例子中,假定每个桶的容量为 2。我们开始按照球 ID 值大小的升序将其分配到桶。 按顺时针移动,1 号球进入桶 C,2 号球进入桶 A,3 号及 4 号球进入桶 B,5 号球进入桶 C。然后 6 号球按顺时针移动尝试进入桶 B, 但由于桶 B 容量已达到限制(容量为 2,此时桶中已装有 3 和 4 号球)。 于是,6 号球继续顺时针移动尝试进入桶 C,但桶 C 也已满了。 最后 6 号球进入了还有空余容量的桶 A。
系统进行任何更新(球或桶插入/删除)时,需要重新计算分配以保证均匀性。算法中巧妙的一点在于,小范围的更新(少量球或桶的插入和删除)只会引起微小的分配变化,以满足一致性目标。在我们的论文中,我们展示了移除或插入一个球引起其他球以 O(1/ε^2) 移动。最重要的一点是,负载上限与系统中的球或桶的总数无关。因此,即是球或桶的数量加倍,负载边界也不会改变。这一点增强了分配问题的可伸缩性(即使扩大分配规模,也不影响一致性)。下图模拟了当桶/服务器发生更新时,移动(再分配)次数随更新的变化情况。
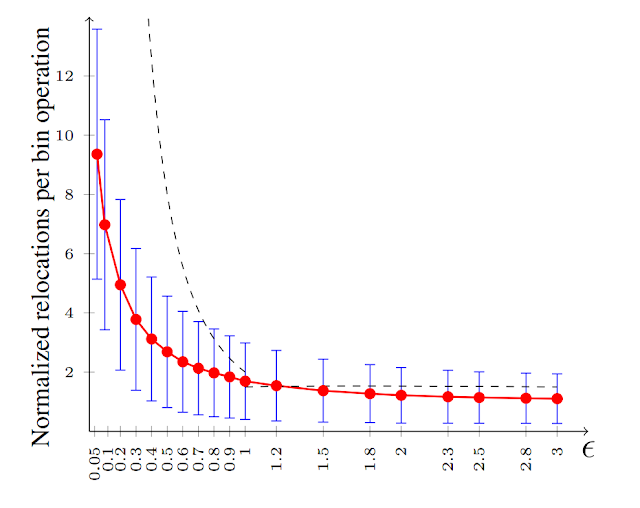
红色曲线表示平均移动次数,蓝色条形表示不同 ε 值(x 轴)的方差。 虚线曲线是我们的理论研究建议的负载上限,它非常适合作为对实际移动次数的预测。 此外,对于任意 ε,我们知道每个桶的负载上下界为平均负载的 (1+ε) 倍。 下图我们看到 ε=0.1、ε=0.3 和 ε=0.9 不同值的对应桶的负载分布。
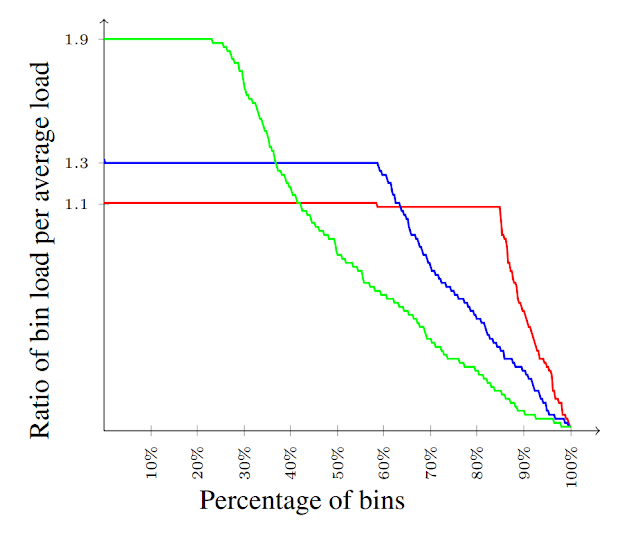
ε 值的负载分布。负载。是均匀的,覆盖了从 0 到 (1+ε) 倍的平均负载,以及许多桶的负载等于 (1+ε) 倍的平均负载
从图中可以看出均匀性和一致性的一个折中——较小的 ε 增强了均匀性,但降低了一致性,而较大的 ε 值提升了一致性而降低了均匀性。较低的 ε 值确保许多桶的负载等于(1+ε)倍平均负载,其余桶的负载则依次衰减。
提供内容托管服务必须准备好,面对差异很大的各种场景。在这种情况下,这种一致的哈希方案是理想的选择,即使在最坏的情况下也表现良好。
虽然我们的内部结果令人振奋,但我们更高兴的是,更广泛的社区发现我们的解决方案足够有用,可以开放源代码,允许任何人使用该算法。 如果您对这项研究的更多细节感兴趣,请参阅 ArXiv 上的论文,并请继续关注 算法与优化团队的更多研究!